Relación entre Comprensión Lectora y Resolución de Problemas Matemáticos en Estudiantes de Primero a Undécimo Grado[1]
Relationship between Reading Comprehension and Mathematical Problem Solving in Students from First to Eleventh Grade
Relação entre Compreensão de Leitura e Resolução de Problemas Matemáticos em Estudantes do Primeiro ao Décimo Primeiro Ano
Willmer Obed Funeme San Martín*[2], Eloy Ramírez de León*[3], Lizeth Paola Pinilla Sánchez*[4]
Corporación Universitaria Adventista de Colombia, Colombia*
Fecha de Recepción: 5-6-2025. Fecha de Aceptación: 23-10-2025
Autor de correspondencia: Willmer Obed Funeme San Martín, [email protected]
Cómo citar:
Funeme S. M., W. O.; Ramírez D-L., E. y Pinilla S., L. P. (2025). Relación entre comprensión lectora y resolución de problemas matemáticos en estudiantes de primero a undécimo grado. Revista Científica Cuadernos de Investigación, 3, e54, 1-18. https://doi.org/10.59758/rcci.2025.3.e54
Resumen
Objetivo: El estudio tuvo como propósito analizar la relación entre la comprensión lectora y el rendimiento en la resolución de problemas matemáticos en estudiantes del Colegio Adventista Libertad de Bucaramanga, Santander. Metodología: Se empleó un enfoque cuantitativo, no experimental, transversal y correlacional. De una población de 1248 estudiantes de primaria a bachillerato, se tomó una muestra aleatoria de 248 participantes. En noviembre de 2024 se aplicaron pruebas estandarizadas de comprensión lectora y resolución de problemas. Los resultados se analizaron mediante estadísticas descriptivas, pruebas de normalidad, correlaciones no paramétricas, ANOVA, Kruskal-Wallis y prueba post hoc de Tukey. Resultados: La comprensión lectora tuvo una media de 100.1 (rango 50–131) y la resolución de problemas una media igual (rango 65–160). No se halló una correlación lineal significativa entre ambas variables; sin embargo, los estudiantes con alta comprensión lectora obtuvieron puntajes superiores en resolución de problemas respecto a quienes presentaron nivel medio (diferencia media = 7.129; p = 0.009). Conclusiones: Se determina que, aunque no existe una relación lineal directa, un mayor nivel de comprensión lectora se asocia con mejor desempeño matemático, lo que evidencia una relación categórica influida por umbrales de competencia.
Palabras clave: comprensión lectora, resolución de problemas, competencias cognitivas, rendimiento académico, correlación.
Abstract
Objective: The study aimed to analyze the relationship between reading comprehension and performance in mathematical problem-solving among students at Colegio Adventista Libertad in Bucaramanga, Santander. Methodology: A quantitative, non-experimental, cross-sectional, and correlational approach was employed. From a population of 1,248 students ranging from elementary to high school, a random sample of 248 participants was selected. In November 2024, standardized tests in reading comprehension and problem-solving were administered. The results were analyzed using descriptive statistics, normality tests, nonparametric correlations, ANOVA, Kruskal–Wallis, and the Tukey post hoc test. Results: Reading comprehension had a mean of 100.1 (range 50–131), and problem-solving performance showed the same mean (range 65–160). No significant linear correlation was found between the two variables; however, students with high reading comprehension scored significantly higher in problem-solving than those with a medium level (mean difference = 7.129; p = 0.009). Conclusions: Although no direct linear relationship was found, a higher level of reading comprehension is associated with better mathematical performance, indicating a categorical relationship influenced by proficiency thresholds.
Keywords: reading comprehension, problem solving, cognitive competencies, academic performance, correlation.
Resumo
Objetivo: O estudo teve como propósito analisar a relação entre a compreensão leitora e o desempenho na resolução de problemas matemáticos em estudantes do Colégio Adventista Liberdade, localizado em Bucaramanga, Santander. Metodologia: Foi adotada uma abordagem quantitativa, não experimental, transversal e correlacional. De uma população de 1.248 estudantes do ensino fundamental ao médio, foi selecionada uma amostra aleatória de 248 participantes. Em novembro de 2024, foram aplicados testes padronizados de compreensão leitora e resolução de problemas. Os resultados foram analisados por meio de estatísticas descritivas, testes de normalidade, correlações não paramétricas, ANOVA, Kruskal-Wallis e teste post hoc de Tukey. Resultados: A compreensão leitora apresentou média de 100,1 (faixa 50–131) e a resolução de problemas a mesma média (faixa 65–160). Não foi encontrada correlação linear significativa entre as duas variáveis; contudo, os estudantes com alta compreensão leitora obtiveram pontuações significativamente maiores na resolução de problemas em comparação àqueles com nível médio (diferença média = 7,129; p = 0,009). Conclusões: Conclui-se que, embora não exista uma relação linear direta, níveis mais altos de compreensão leitora estão associados a um melhor desempenho matemático, indicando uma relação categórica influenciada por limiares de competência.
Palavras Chave: compreensão de leitura, resolução de problemas, competências cognitivas, desempenho acadêmico, correlação.
Durante los últimos años, el sector de la educación ha tenido un firme interés de identificar con precisión cuál es la relación entre la comprensión lectora y el rendimiento en la resolución de problemas matemáticos (Nahdi et al., 2023). Esto se debe a la relevancia que puede tener para el desarrollo integral del estudiante, así como al impacto directo que ejerce sobre las políticas educativas gubernamentales en materia de calidad, con el fin de formar individuos competentes y adaptables (Can, 2020). Tras analizar varios estudios relacionados con el tema, se establece que, posiblemente, el 65 % de los errores al ejecutar adecuadamente la resolución de problemas matemáticos tiene su origen en la mala interpretación de los enunciados presentados (Antezana y Guarachi, 2021; Hijada & Dela Cruz, 2023; Khalid & Embong, 2020; Prasetyaningrum & Yuniarti, 2021).
Este fenómeno evidencia la potencial interdependencia entre las competencias lingüísticas y el razonamiento matemático. Por tal motivo, este trabajo indaga esta particular relación de manera específica en el Colegio Adventista Libertad (COAL) de Bucaramanga, Colombia, donde las evaluaciones internas y externas realizadas en los tres últimos años revelan que el aproximadamente un 58% de los estudiantes presentan algún tipo de dificultad de manera simultánea en estas áreas.
La comprensión lectora, según Sánchez (2013) y Valero-Ancco et al. (2024), puede entenderse como la habilidad que abarca el entendimiento de lo que se lee e involucra el uso adecuado de los significados de las palabras para identificar la idea global del texto y construir conocimientos. Por otro lado, la resolución de problemas matemáticos requiere de una destreza metodológica, según Díaz y Díaz (2018), y Pérez y Ramírez (2011), que sea útil para identificar, actuar y proceder de manera ordenada con los elementos numéricos, lo que permite solucionar problemas de forma precisa y reflexiva. Por lo cual, Nahdi et al. (2023) reconocen que estas dos competencias facilitan el acceso a una amplia gama de conocimientos y permite interaccionar con la información compleja de la realidad desde su aplicación al usar conceptos abstractos en situaciones concretas y que son esenciales para alcanzar el éxito académico, el pensamiento analítico y el desarrollo integral del estudiante en el escenario académico actual.
Los estudios globales sobre el tema destacan que la capacidad para decodificar y comprender apropiadamente los textos es un elemento predictor clave para alcanzar un óptimo rendimiento matemático (López, 2021; Romero, 2012). Así, la comprensión lectora juega un papel determinante en el escenario escolar. Esto permite al estudiante analizar de manera pertinente los casos que involucran situaciones que requieran resolución de casos matemáticos y ejecutarlos apropiadamente. Asimismo, se evidencia que los resultados que los estudiantes obtienen en los exámenes funcionan como indicadores de la calidad educativa institucional. Esto se manifiesta particularmente en el desempeño que tuvo Colombia en el informe del Programa para la Evaluación Internacional de los Estudiantes o informe PISA 2022, donde alcanzó la puntuación de 383 en Matemáticas y 409 en Lectura, que lo llevó a ocupar el puesto 64 entre 81 países participantes de la Organización para la Cooperación y el Desarrollo Económicos (OCDE). Al comparar los resultados de Colombia con el promedio alcanzando por los países de la OCDE (Matemáticas 472 y Lectura 476), se identifican bajas puntuaciones en las dos áreas, lo cual, según el mismo informe generado por la OCDE (2023), evidencia las dificultades que los estudiantes siguen teniendo en la lectura y cómo esto repercute directamente en la forma de entender y aplicar los conceptos matemáticos debidamente, y como consecuencia se manifiesta en los resultados derivados. De esta forma, la correlación entre el pensamiento matemático y la comprensión lectora subraya que ambas habilidades, interdependientes, son esenciales para el desarrollo de competencias cognitivas de orden superior.
En el COAL, después de considerar cuidadosamente los registros académicos de las pruebas externas e internas realizadas durante los años 2022-2024 entre estos dos componentes, se llegó a identificar que aproximadamente el 58% de las deficiencias en las evaluaciones matemáticas realizadas a los estudiantes llegan a revelar una tendencia generalizada a fallos en la interpretación de enunciados. Esto se da particularmente en aquellos problemas que requieren una inferencia de datos implícitos, o que por, otro lado, requieren de la aplicación de múltiples operaciones matemáticas. Se puede agregar, además, que el problema particular de este estudio se origina por las observaciones recurrentes realizadas por los docentes desde el aula, en donde se identifica que los estudiantes del COAL enfrentan desafíos persistentes entre estas dos áreas. Estas dificultades se manifiestan en las actividades donde hay interpretación de enunciados problemáticos y la aplicación de conceptos matemáticos, lo que plantea la pregunta de investigación que pretende medir si ¿existe una relación significativa entre la comprensión lectora y el rendimiento en la resolución de problemas matemáticos en los estudiantes del Colegio Adventista Libertad de Bucaramanga? Estudios como los de Antezana y Guarachi (2021) y Snow & Sweet (2003), indican que la lectura deficiente puede ser un elemento que impida la plena comprensión de problemas matemáticos y limiten el buen rendimiento académico.
De acuerdo con lo anterior, este estudio considera en su hipótesis alternativa que existe una relación entre estas habilidades en los estudiantes que cursan el grado primero hasta undécimo en el COAL de Bucaramanga. Esta interconexión entre estas áreas del saber se establece de acuerdo con lo planteado por Akın (2022), Terrones et al. (2023), Kintsch (1998), Schoenfeld (1992) y Vinces et al. (2024), quienes declaran una relación significativa entre ambas competencias, lo cual da pertinencia y una base sólida a esta investigación que se centra en explorar y determinar cuantitativamente las anteriores variables en un contexto determinado. Investigaciones de carácter internacional como las de Snow & Sweet (2003) y nacionales como las de Jiménez (2023) y Valdez-Asto (2021) presentan resultados serios de una correlación positiva entre comprensión lectora y el desempeño matemático, sugiriendo que una buena lectura facilita la resolución de problemas complejos.
Sin embargo, se identificaron estudios en donde hay factores que moderan la relación anterior. La literatura científica analizada identifica varios factores que pueden moderar o influir en la fuerza y la naturaleza de la relación entre la comprensión lectora y la resolución de problemas matemáticos. Por ejemplo, Akın (2022) indica que las diferentes habilidades matemáticas pueden interactuar de manera distinta con la comprensión lectora. De esta manera, la resolución de problemas como habilidad matemática específica demuestra la asociación más fuerte con la comprensión lectora, mientras que otras habilidades, como el razonamiento espacial, pueden exhibir una conexión más débil. Por otro lado, Anselmo (2017) y Bae et al. (2015) identifican que la comprensión lectora puede afectar los diferentes dominios del contenido matemático en los diversos grados, es decir, no ser necesaria. Los indicadores como la edad y la etapa de desarrollo de los estudiantes juegan un papel importante al tener en consideración desde las características específicas de los estudiantes, incluida la presencia de discapacidades de aprendizaje y el nivel de dominio del idioma, también pueden influir en esta relación.
Así mismo hay estudios que presentan conclusiones donde se evidencia que no hay correlación significativa. Si bien se puede encontrar una gran cantidad de investigaciones que apoyan sustancialmente esta relación de forma positiva, algunos estudios recientes han llegado a la conclusión de hallar una correlación débil o incluso no significativa entre la comprensión lectora y la resolución de problemas matemáticos. Como sustento de esto, las investigaciones de Acharya (2017) y Obina et al. (2025) sugieren que hay otros factores que se deben considerar como el conocimiento matemático específico del estudiante, el dominio de las estrategias de resolución de problemas que este tenga, su competencia aritmética básica adquirida durante los años previos, su nivel de motivación y concentración a la hora de desarrollar la actividad, e incluso las características únicas del lenguaje matemático en sí, podrían ejercer una influencia más dominante en su capacidad para resolver problemas matemáticos. Además, Klotz et al. (2025) destacan el impacto significativo de la complejidad lingüística inherente a las tareas matemáticas en el rendimiento de los estudiantes.
Teniendo en consideración lo anterior, se establece el objetivo general de este estudio que es determinar la relación entre la comprensión lectora y el rendimiento en la resolución de problemas matemáticos en los estudiantes del Colegio Adventista Libertad de Bucaramanga. Para alcanzar este propósito, se establecen los siguientes objetivos específicos: 1. Evaluar el nivel de comprensión lectora mediante la Prueba 9 ‘Comprensión de Textos’ de la Batería III Woodcock-Muñoz (Woodcock & Muñoz-Sandoval, 2001); 2. Medir el rendimiento en la resolución de problemas matemáticos utilizando la Prueba 10 ‘Problemas Aplicados’ de la misma batería; 3. Analizar si existe una correlación entre los puntajes obtenidos en ambas pruebas; y, 4. Proponer recomendaciones pedagógicas basadas en los resultados obtenidos, orientadas a mejorar ambas competencias.
La relevancia de esta investigación radica en la posibilidad de mejorar la calidad educativa en el COAL al exponer evidencia empírica sobre la conexión entre dos áreas fundamentales del currículo escolar. De acuerdo con los postulados de Díaz y Hernández (2010), para transformar los paradigmas educativos solo se requiere la capacidad de comprender las interacciones entre aquellas habilidades fundamentales y las necesidades educativas locales. En el ámbito nacional e internacional, la identificación y análisis de los resultados puede ayudar a entender la función de estas competencias con la intención de orientar la acción pedagógica de los docentes y directivos para intervenir en el diseño de estrategias que fortalezcan ambas habilidades, reduciendo brechas en el aprendizaje y optimizando el rendimiento académico.
Metodología
El presente estudio, de acuerdo con su objetivo general y la pregunta que se desea responder, utilizó un enfoque cuantitativo con el propósito de determinar objetivamente la relación entre la comprensión lectora y la resolución de problemas matemáticos en estudiantes del Colegio Adventista Libertad, ubicado en Bucaramanga, Santander, Colombia.
El tipo de investigación fue correlacional, no experimental, con un diseño de corte transversal. Al ser no experimental, no se manipularon las variables de estudio. El corte transversal implicó que la recolección de datos se diera un único momento específico, en este caso noviembre de 2024, ofreciendo una muestra instantánea del rendimiento estudiantil en ese período. Así mismo, el tipo de estudio correlacional permitió medir e identificar las asociaciones estadísticas entre la comprensión lectora (variable independiente) y la resolución de problemas matemáticos (variable dependiente) sin establecer relaciones de causalidad.
Por otra parte, la población objetivo de este estudio estuvo constituida por los 1248 estudiantes debidamente matriculados en el año 2024 en el colegio Adventista Libertad de Bucaramanga. De esta población se sacó la muestra que estuvo compuesta por estudiantes de primero a undécimo grado abarcando todos los niveles, donde se seleccionaron a 248 de ellos, elegidos mediante un muestreo aleatorio simple por cada curso. Además, se consideró el rango de edades y las habilidades de los estudiantes de cada curso para determinar el tamaño muestral con la finalidad de mantener la representatividad en la correlación de las variables y garantizar la significación estadística de los resultados.
La Batería III Woodcock-Muñoz (Woodcock y Muñoz-Sandoval, 2001) que es una herramienta estandarizada y validada para la evaluación de competencias cognitivas fue el instrumento seleccionado para recolectar los datos. Se empleó de esta batería la Prueba 9 denominada ‘Comprensión Lectora’ que es útil para medir la habilidad de los estudiantes es situaciones de interpretar y analizar textos de forma estándar. Seguidamente se utilizó la Prueba 10, titulada ‘Problemas Aplicados’ que evaluó la capacidad de los estudiantes para resolver problemas matemáticos prácticos. Las puntuaciones obtenidas mediante la Batería III Woodcock-Muñoz permitieron comparar las variables de interés del estudio. Esta batería ha demostrado adecuados niveles de validez y confiabilidad para la evaluación de las competencias mencionadas en poblaciones escolares. Además, cuenta con un software propio que facilita el análisis e interpretación de los datos. Considerando los estándares de puntuación establecidos por la batería, el procesamiento de los datos se realizó utilizando el software R.
De esta manera, para el análisis de los datos recolectados a través del instrumento utilizado, se empleó el software R Core Team (2021) que opera bajo el entorno del lenguaje R. Los datos y sus resultados se analizaron y estructuraron en varias fases analíticas. En primer lugar, con el fin de caracterizar el rendimiento general de la muestra se procedió a realizar el respectivo análisis descriptivo con las puntuaciones recolectadas en bruto de acuerdo a los datos suministrados por los estudiantes mediante la aplicación de las pruebas 9 y 10 de la Batería III Woodcock. Al ponderar el desempeño de los estudiantes en ambas variables mediante las medidas de la media, mediana y desviación estándar se llegó a percibir la variabilidad de los datos en conjunto.
En segundo lugar, con la intención de identificar si los datos seguían una distribución normal, se empleó la prueba de normalidad Shapiro-Wilk. Este procedimiento examinó las puntuaciones estandarizadas en comprensión lectora y resolución de problemas indicando que los datos recolectados no seguían una distribución normal, lo que requirió el uso de métodos estadísticos no paramétricos.
En tercer lugar, con el objetivo de comprobar si existía una relación significativa entre la comprensión lectora y la resolución de problemas presentadas en la hipótesis alternativa (Existe una relación significativa entre la comprensión lectora y la resolución de problemas matemáticos) y la hipótesis nula (No existe una relación significativa entre la comprensión lectora y la resolución de problemas matemáticos), se procedió a calcular el coeficiente de correlación Kendall para determinar la fuerza y dirección de la relación entre las variables dada la no normalidad de los datos.
Como procedimiento de soporte, a pesar de la ausencia de una correlación directa significativa, se investigaron las diferencias en el rendimiento en la resolución de problemas entre los distintos grupos según el nivel de comprensión lectora. Para ello, se compararon los datos de los grupos de alto, medio y bajo nivel de comprensión lectora mediante dos pruebas: la prueba no paramétrica de Kruskal-Wallis y el ANOVA (Análisis de Varianza). Finalmente, dado que ambas pruebas, cuyos datos preliminares sugerían una relación débil entre las variables, indicaron diferencias significativas, se realizó la prueba de Tukey para identificar específicamente entre qué pares de grupos existían dichas diferencias.
En cuanto a los aspectos éticos, se obtuvo la autorización de la dirección del Colegio Adventista Libertad para la realización del estudio. Se informó a los estudiantes y a sus padres acerca de los objetivos de la investigación y se garantizó la confidencialidad y el anonimato de los datos recolectados. La participación fue voluntaria, y se les notificó que podían retirarse en cualquier momento sin que ello implicara consecuencias.
Resultados
Con la intención de determinar cuál es la principal relación entre la comprensión lectora y el rendimiento en la resolución de problemas matemáticos en los estudiantes del Colegio Adventista Libertad de Bucaramanga, se presenta el siguiente análisis a partir de la revisión estadística de los datos recolectados.
Análisis descriptivo
A continuación, se describen los resultados descriptivos de las puntuaciones estándar obtenidas por medio de las pruebas de Comprensión Lectora y Resolución de Problemas Matemáticos de la Batería III Woodcock-Muñoz aplicadas a los estudiantes de primero a undécimo del Colegio Adventista Libertad en donde se llega a los siguientes resultados:
· La variable Comprensión Lectora obtiene una puntuación mediana de 101.0. La media arroja una puntuación de 100.1. Además, se identifican que las puntuaciones variaron desde un mínimo de 50 hasta un máximo de 131.
· Para la variable de Resolución de Problemas Matemáticos, la mediana es de 98.0. La media está conformada con 100.1. Por tanto, el rango de puntuaciones en esta prueba fue de 65 a 160.
Lo anterior indica que ambas pruebas mostraron una tendencia central similar, con medias y medianas alrededor de 100 puntos, lo cual es consistente con el valor esperado de la escala estandarizada. En cuanto a la dispersión de los datos se detecta que:
· Para la variable de Comprensión Lectora la puntuación mínima es de 50.0 en relación con la variable de Resolución de Problemas Matemáticos de 65.0, lo que indica un mayor rezago en lectura en algunos casos.
· Consiguientemente, las puntuaciones máximas alcanzadas son para Comprensión Lectora de 131.0 y en Resolución de Problemas Matemáticos de 160.0 lo cual destaca que algunos estudiantes superaron ampliamente el promedio.
· Por otro lado, los cuartiles indican una distribución ligeramente más amplia en matemáticas (máximo de 160 vs 131 en lectura), sugiriendo una mayor variabilidad en el desempeño en esta área en comparación con la comprensión lectora.
A continuación, se presenta un resumen estadístico de las puntuaciones estándar para ambas variables (ver Tabla 1).
Tabla 1. Estadísticas Descriptivas de las Puntuaciones Estándar en Comprensión Lectora y Resolución de Problemas Matemáticos.
|
Variable |
Mín. |
1er Cuartil |
Mediana |
Media |
3er Cuartil |
Máx. |
|
Comprensión Lectora (Y) |
50.0 |
92.0 |
101.0 |
100.1 |
110.0 |
131.0 |
|
Resolución de Problemas Matemáticos (X) |
65.0 |
89.0 |
98.0 |
100.1 |
108.0 |
160.0 |
Fuente: Elaboración propia. Nota: Las medianas y medias cercanas (alrededor de 100) sugieren una distribución simétrica, aunque Resolución de Problemas Matemáticos muestra un rango mayor (65.0-160.0) en comparación con Comprensión Lectora (50.0-131.0).
Las medianas y medias cercanas (alrededor de 100) en ambas variables (‘Comprensión Lectora’ y ‘Resolución de Problemas Matemáticos’) indican que los datos tienden a tener una distribución simétrica, probablemente cercana a una distribución normal, sin sesgos marcados hacia valores extremos. Esto sugiere que la mayoría de los estudiantes tienen puntuaciones agrupadas alrededor del valor central (aproximadamente 100), lo cual es típico en escalas estandarizadas donde 100 suele ser la media esperada.
Sin embargo, el rango mayor en ‘Resolución de Problemas Matemáticos’ (65.0 a 160.0) en comparación con ‘Comprensión Lectora’ (50.0 a 131.0) implica una mayor variabilidad en los puntajes de esta variable. Esto podría indicar que los estudiantes muestran diferencias más pronunciadas en su habilidad para resolver problemas matemáticos, posiblemente por la complejidad de las tareas, la diversidad en las estrategias de resolución o diferencias en la preparación académica. En contraste, las puntuaciones en ‘Comprensión Lectora’ son más uniformes, lo que sugiere una consistencia relativa en el desempeño en esta área.
Posteriormente, los estudiantes fueron clasificados en los varios niveles de desempeño para cada variable teniendo en cuenta la tabla de original de clasificación de la Batería. Pero se requirió realizar una reclasificación simplificada de estos niveles de desempeño en tres categorías amplias (Bajo, Medio, Alto) con el fin de que este procedimiento facilitará el análisis, la interpretación de los resultados y la identificación de tendencias de acuerdo a las puntuaciones estándar obtenidas. La distribución de frecuencias-porcentajes de los estudiantes en estos niveles se presenta en la Tabla 2.
Tabla 2. Distribución de Frecuencias y Porcentajes de los Niveles de Desempeño en Comprensión Lectora y Resolución de Problemas Matemáticos (N=247).
|
Variable |
Nivel de Desempeño |
Frecuencia (n) |
Porcentaje (%) |
|
Comprensión Lectora |
Bajo |
60 |
24.3 |
|
|
Medio |
134 |
54.2 |
|
|
Alto |
53 |
21.5 |
|
TOTAL |
|
247 |
100 |
|
Resolución de Problemas Matemáticos |
Bajo |
63 |
25.5 |
|
Medio |
136 |
55.1 |
|
|
Alto |
48 |
19.4 |
|
|
TOTAL |
|
247 |
100 |
Fuente: Elaboración propia. Nota. La mayoría de los estudiantes se encuentran en el nivel Medio tanto en Comprensión Lectora (54.2%) como en Resolución de Problemas Matemáticos (55.1%), mientras que menos del 22% alcanzan el nivel Alto en ambas variables.
Se debe puntualizar que esta reclasificación no altera la validez del análisis original, sino que agrupa niveles adyacentes de rendimiento para facilitar la interpretación y el análisis comparativo en el marco de este estudio. La distribución porcentual de esta reclasificación está expuesta de manera gráfica en las Figuras 1 y 2.
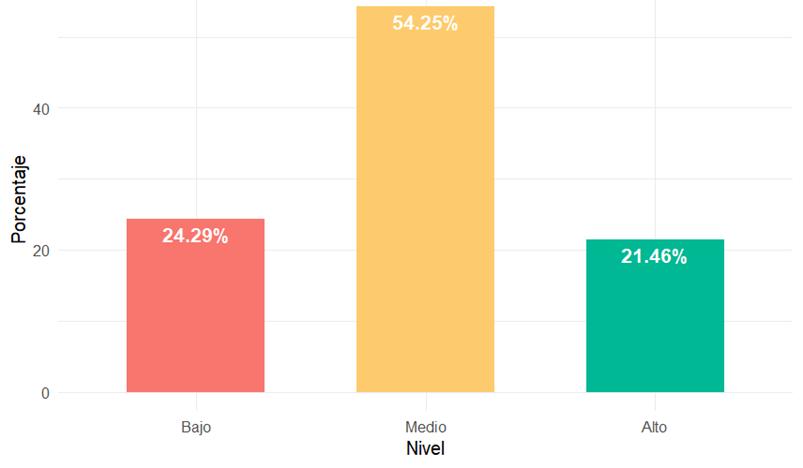
Figura 1. Niveles de Comprensión Lectora.
Fuente: Elaboración propia. Nota. La figura muestra la distribución porcentual en tres niveles: Bajo (24.29%), Medio (54.25%) y Alto (21.46%).
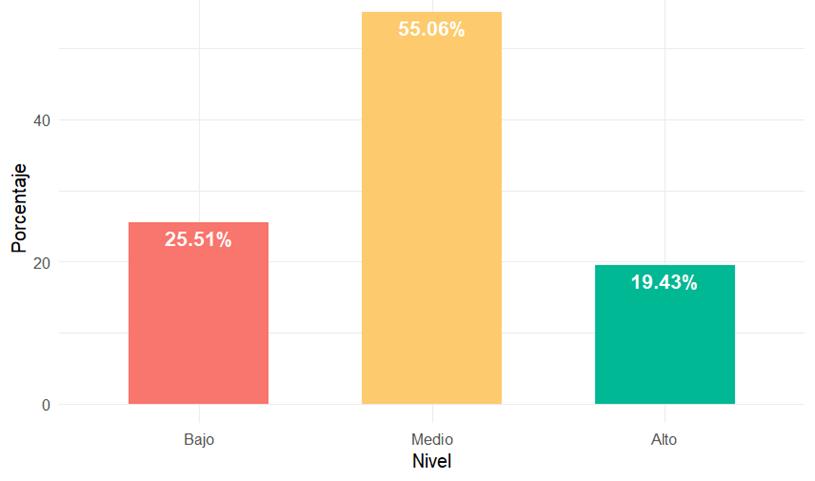
Figura 2. Niveles de Resolución de Problemas Matemáticos
Fuente: Elaboración propia. Nota. La figura muestra la distribución porcentual en tres niveles: Bajo (25.51%), Medio (55.06%) y Alto (19.43%).
Pruebas de normalidad
Se aplicó la prueba de Shapiro-Wilk para evaluar la normalidad de las distribuciones de las puntuaciones estándar en comprensión lectora y resolución de problemas matemáticos.
- Para la puntuación estándar en resolución de problemas matemáticos se obtuvo los resultados de W = 0.97779, p-valor = 0.0006514 (p<.001).
- Para la puntuación estándar en comprensión lectora el resultado fue de W = 0.94839, p-valor = 1.135e-07 (p<.001).
Dado que en ambos casos los p-valores fueron menores a 0.05, se concluyó que las variables y las distribuciones de las puntuaciones no se ajustaban a una distribución normal. Estos resultados justificaron el uso de pruebas no paramétricas para los análisis inferenciales subsiguientes (ver Tabla 3).
Tabla 3. Comparación de Estadísticos W (Shapiro-Wilk)
|
Variable Analizada |
Estadístico W |
p-valor |
¿Distribución Normal? |
|
Comprensión Lectora |
0.948 |
1.135e-07 < .001 |
No |
|
Resolución de Problemas Matemáticos |
0.978 |
0.0006514 < .001 |
No |
Fuente: Elaboración propia. Nota: Un p-valor < 0.05 en la prueba de Shapiro-Wilk sugiere que los datos no se distribuyen normalmente.
Análisis de correlación
Para investigar la relación entre la comprensión lectora y la resolución de problemas matemáticos, se utilizaron el coeficiente de correlación de rangos de Kendall (τ). Los resultados se detallan en la Tabla 4.
Tabla 4. Coeficientes de Correlación entre Comprensión Lectora y Resolución de Problemas Matemáticos.
|
Prueba de Correlación |
Variable 1 |
Variable 2 |
Coeficiente |
Valor p |
|
Kendall |
Comprensión Lectora |
Resolución de Problemas |
τ=0.053 |
0.2387 |
Fuente: Elaboración propia. Nota. Los valores p > 0.05 indican que no hay correlación significativa entre Comprensión Lectora y Resolución de Problemas Matemáticos según la prueba Kendall (p = 0.2387).
Los coeficientes de correlación obtenidos fueron muy bajos y los valores p asociados (Spearman: p=0.2807; Kendall: p=0.2387) fueron superiores al nivel de significancia de 0.05. Estos resultados indican que no se encontró una correlación estadísticamente significativa entre las puntuaciones de comprensión lectora y las de resolución de problemas matemáticos en la muestra estudiada. La Figura 3 ilustra la distribución de los datos y la ausencia de una tendencia lineal clara.
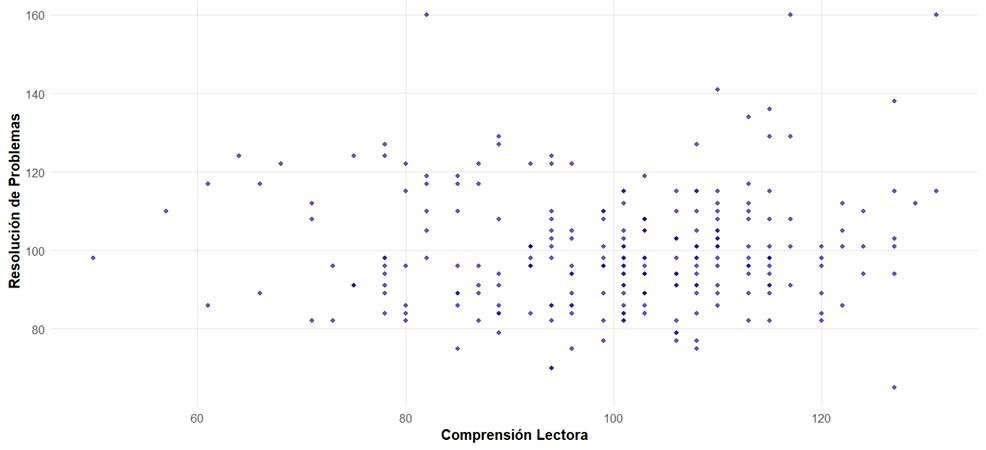
Figura 3. Gráfico de dispersión entre comprensión lectora y resolución de problemas.
Fuente: Elaboración propia. Nota: La grafica muestra a cada estudiante como un punto. Comprensión Lectora en el eje X y Resolución de Problemas en el eje Y. Las puntuaciones estándar de ambas variables indican distribución no constante.
Comparación del rendimiento entre variables
A pesar de la ausencia de una correlación lineal significativa, se exploró si existían diferencias en el rendimiento en resolución de problemas matemáticos entre los distintos grupos de comprensión lectora (Bajo, Medio, Alto). Para ello, se utilizaron la prueba de Kruskal-Wallis (no paramétrica) y ANOVA (paramétrica, para contraste), seguida de una prueba post hoc de Tukey.
La prueba de Kruskal-Wallis reveló diferencias estadísticamente significativas en las medianas de las puntuaciones de Resolución de Problemas entre los tres grupos de Comprensión Lectora (X2(2) = 6.678, p=0.035). De manera similar, el Análisis de Varianza (ANOVA) de un factor también mostró un efecto significativo del nivel de Comprensión Lectora sobre las puntuaciones de Resolución de Problemas (F (2,244) = 4.422, p=0.013). Los resultados de estas pruebas se resumen en la Tabla 5.
Tabla 5. Resultados de las Pruebas de Kruskal-Wallis y ANOVA para la Comparación de Puntuaciones
|
Prueba Estadística |
Estadístico de Prueba |
Grados de Libertad |
Valor p |
|
Kruskal-Wallis |
X2 = 6.678 |
2 |
0.035∗ |
|
ANOVA |
F=4.422 |
2,244 |
0.013∗ |
Fuente: Elaboración propia. Nota: * p<0.05 indica que existen diferencias significativas en la puntuación de resolución de problemas matemáticos entre al menos dos de los grupos de comprensión lectora.
Por otra parte, para identificar las diferencias específicas entre los pares de grupos, se realizó una prueba post hoc de Tukey HSD, cuyos resultados se presentan en la Tabla 6.
Tabla 6. Resultados de la prueba post hoc de Tukey para diferencias en resolución de problemas entre grupos de comprensión lectora
|
Comparación de Grupos |
Diferencia de Medias |
Intervalo de Confianza (95%) |
Valor p ajustado |
||
|
Medio - Bajo |
−3.121 |
[−8.380,2.137] |
0.3427 |
||
|
Alto - Bajo |
+4.007 |
[−1.521,9.535] |
0.2037 |
||
|
Alto - Medio |
7+.129 |
[1.475,12.782] |
0.0090∗∗ |
||
Fuente: Elaboración propia. Nota. p < 0.05 indica significancia estadística. Elaboración propia de acuerdo a los datos recolectados y analizados con el software R Core Team (2021).
La prueba de Tukey HSD indicó que los estudiantes con un nivel Alto de Comprensión Lectora obtuvieron puntuaciones significativamente más altas en Resolución de Problemas Matemáticos en comparación con los estudiantes con un nivel Medio de Comprensión Lectora (diferencia de medias = 7.129, p=0.009). No se encontraron diferencias estadísticamente significativas entre los grupos Medio y Bajo (p=0.343), ni entre los grupos Alto y Bajo (p=0.204). Estas diferencias entre grupos pueden observarse visualmente en la Figura 4.
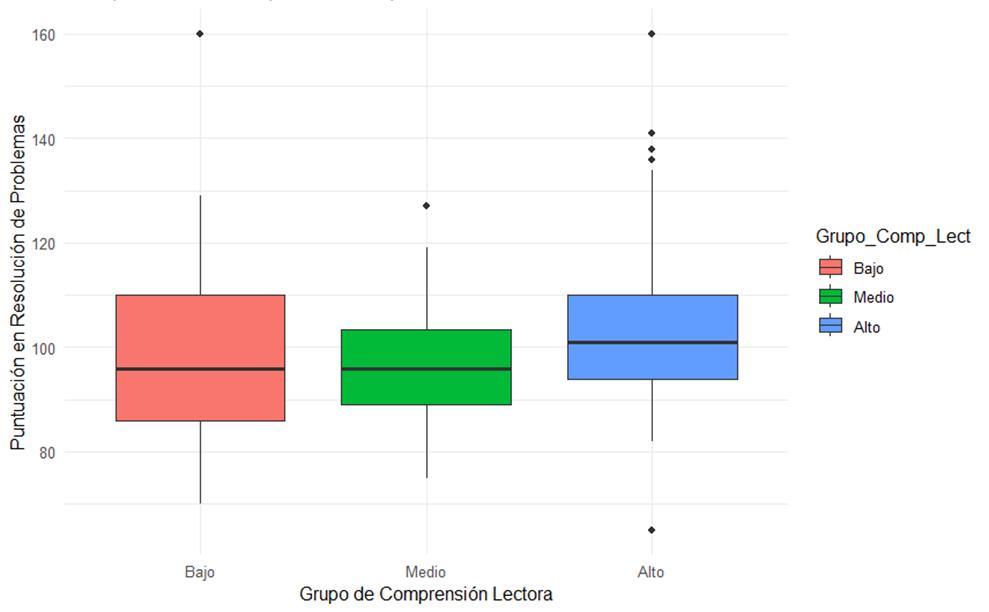
Figura 4. Diagrama de Cajas de las Puntuaciones de Resolución de Problemas Matemáticos según Nivel de Comprensión Lectora
Fuente: Elaboración propia. Nota. Los diagramas de cajas muestran la distribución de las puntuaciones en Resolución de Problemas Matemáticos para cada nivel de Comprensión Lectora. Los puntos fuera de las cajas indican valores atípicos, y las líneas dentro de las cajas representan las medianas.
El diagrama de cajas (Figura 4) muestra que, aunque existe solapamiento entre las distribuciones, la mediana de las puntuaciones en Resolución de Problemas tiende a ser mayor a medida que aumenta el nivel de Comprensión Lectora (Mediana Grupo Bajo ≈ 95; Mediana Grupo Medio ≈ 97; Mediana Grupo Alto ≈ 105). El grupo Alto también muestra algunos valores atípicos superiores. Esto se alinea con los resultados de la Tabla 3 (coeficientes de correlación no significativos, p > 0.05), que mostraron que no hay una correlación estadísticamente significativa entre estas variables.
En resumen, los resultados no mostraron una correlación lineal significativa entre la comprensión lectora y la resolución de problemas matemáticos. Sin embargo, se encontraron diferencias significativas en el rendimiento en resolución de problemas cuando se compararon los grupos por nivel de comprensión lectora, específicamente entre los estudiantes de nivel alto y medio de comprensión.
Discusión
La revisión de la bibliografía consultada muestra puntos de coincidencia y aproximación entre las investigaciones realizadas en diferentes contextos latinoamericanos y europeos que refuerzan la interdependencia entre comprensión lectora y desempeño matemático, especialmente en problemas que requieren interpretación y elaboración de inferencias de este orden. De acuerdo con lo anterior, los hallazgos de Carballo (2024) y Montero y Mahecha, (2020) llegan a mostrar una correlación significativamente alta entre estas dos competencias por lo cual resaltan que fortalecer las habilidades lectoras en el estudiante tiene un impacto considerable en el razonamiento matemático que les permite tener un desempeño alto en la resolución de problemas matemáticos. Por lo cual, a través del análisis de varianza (ANOVA) (F (2, 244) = 4.422, p = 0.013) y la prueba no paramétrica de Kruskal-Wallis (χ² = 6.6784, p = 0.03547) se confirma estadísticamente la existencia de variaciones significativas en el desempeño matemático entre distintos grupos de competencia lectora que al complementarse con la prueba post hoc de Tukey arroja resultados significativos donde se evidencia que los estudiantes con un alto nivel de comprensión lectora alcanzan resultados significativamente más altos en resolución de problemas matemáticos respecto a los de nivel medio (p = 0.0090661).
Por otro lado, algunos estudios marcan distanciamientos, señalando que la relación entre estas habilidades no siempre alcanza significación estadística. Investigadores como Acharya (2017) y Obina et al. (2025) destacan que existen factores adicionales —como el dominio de estrategias matemáticas, la motivación y las particularidades del lenguaje matemático— que median esta relación. Además, la literatura advierte que la complejidad lingüística en los enunciados matemáticos puede influir de manera más determinante que la habilidad lectora por sí sola. De esta forma, el análisis de correlación no paramétrico (Kendall τ=0.0526, p=0.2387) refuerza la idea de que no existe una relación monotónica clara entre ambas variables. Esto invita a reconsiderar la supuesta correspondencia directa asumida en modelos educativos tradicionales y sugiere que comprensión lectora y resolución de problemas matemáticos pueden operar de manera parcialmente independiente, aunque la presencia de umbrales de desempeño y diferencias grupales advierten una relación compleja y dinámica entre ambas competencias.
La aparente contradicción de no detectarse una correlación lineal y la presencia de diferencias significativas entre grupos plantea que la relación entre comprensión lectora y habilidades matemáticas es más intrincada que un mero patrón lineal o monotónico. Podría tratarse de una relación compleja, manifestándose quizás de manera escalonada o categórica. El análisis del boxplot respalda esta interpretación, mostrando un incremento en las medianas de desempeño matemático conforme mejora el nivel de comprensión lectora (Bajo ≈ 95, Medio ≈ 97, Alto ≈ 105). La identificación de diferencias en los hallazgos de los grupos seleccionados, aunque los resultados de correlación no muestran una relación lineal significativa sugiere que, si hay una asociación entre estas habilidades cognitivas parcialmente, lo que coincide con la literatura que señala conexiones entre habilidades lingüísticas y matemáticas. Esta dualidad en los resultados (no correlación, pero sí diferencia entre grupos) puede explicarse entendiendo que diferentes análisis estadísticos capturan distintos aspectos de la relación entre variables.
La diferencia significativa encontrada específicamente entre los grupos de comprensión lectora alta y media, pero no entre alta y baja o media y baja, sugiere una posible relación umbral, donde el impacto de la comprensión lectora sobre la resolución de problemas matemáticos podría manifestarse más claramente al alcanzar niveles superiores de competencia lectora. Estos resultados tienen importantes implicaciones teóricas y prácticas. En términos teóricos, cuestionan la asunción simplista de una relación lineal entre competencias lingüísticas y matemáticas, sugiriendo en cambio interacciones más complejas que podrían depender de umbrales de competencia o factores mediadores no identificados en este estudio. En términos prácticos, estos hallazgos sugieren que la mejora en la comprensión lectora podría beneficiar el desempeño en resolución de problemas matemáticos, pero principalmente cuando los estudiantes alcanzan niveles altos de competencia lectora. Esto tiene implicaciones para el diseño de intervenciones educativas, sugiriendo que las estrategias de fortalecimiento en comprensión lectora no tendrían un impacto uniforme en el desempeño matemático para todos los estudiantes.
El presente estudio tiene algunas limitaciones que deben considerarse al interpretar los resultados. En primer lugar, las puntuaciones estandarizadas utilizadas permiten comparaciones válidas, pero podrían enmascarar aspectos cualitativos de la relación entre estas habilidades. Segundo, la clasificación en tres niveles de desempeño, aunque justificada estadísticamente, implica una simplificación que podría no capturar matices importantes en la progresión de las habilidades. Adicionalmente, los análisis realizados identifican asociaciones estadísticas, pero no establecen relaciones causales entre la comprensión lectora y la resolución de problemas matemáticos. Factores no medidos como habilidades cognitivas generales, motivación, estrategias de aprendizaje o variables socioeconómicas podrían estar mediando o moderando estas relaciones.
Futuras investigaciones podrían beneficiarse de diseños longitudinales que permitan evaluar cómo cambia la relación entre estas habilidades a lo largo del tiempo y del desarrollo educativo. Asimismo, sería valioso explorar los mecanismos específicos mediante los cuales la comprensión lectora alta contribuye a un mejor desempeño en resolución de problemas matemáticos, posiblemente incorporando análisis cualitativos de estrategias de comprensión y resolución de problemas matemáticos.
También resultaría interesante evaluar si intervenciones enfocadas en mejorar específicamente la comprensión lectora a niveles avanzados tienen un impacto directo en el rendimiento matemático, y si este efecto varía según el tipo de problemas matemáticos presentados (por ejemplo, problemas verbales versus problemas puramente numéricos o espaciales).
Conclusiones
El estudio analizó la relación entre la comprensión lectora y la resolución de problemas matemáticos en estudiantes, encontrando que no existe una correlación lineal significativa entre ambas variables según los coeficientes de Kendall (τ=0.0526). Sin embargo, sí se identificaron diferencias estadísticamente significativas en el desempeño matemático entre grupos con distintos niveles de comprensión lectora, mediante ANOVA (p=0.013) y Kruskal-Wallis (p=0.03547).
Específicamente, los estudiantes con nivel alto de comprensión lectora mostraron un desempeño significativamente mejor en resolución de problemas matemáticos que aquellos con nivel medio (p=0.0090661), con una diferencia media de 7.13 puntos. Esta aparente contradicción revela que la relación entre estas habilidades no es estrictamente lineal o monotónica, sino que podría manifestarse de manera más compleja o categórica.
Con respecto a la hipótesis inicial que planteaba la existencia de una relación significativa entre la comprensión lectora y la resolución de problemas matemáticos, los resultados ofrecen una respuesta matizada. Si bien no se encontró evidencia de una relación lineal directa, sí se identificó una asociación significativa cuando se analizaron los datos desde una perspectiva categórica por niveles de desempeño. Estos hallazgos sugieren que la relación entre comprensión lectora y resolución de problemas matemáticos podría ser más compleja de lo inicialmente planteado, posiblemente involucrando umbrales de competencia, donde el impacto de una habilidad sobre la otra se manifestaría principalmente al alcanzar niveles superiores de dominio.
Los resultados de este estudio tienen implicaciones importantes para la práctica educativa. Sugieren que el desarrollo de habilidades avanzadas de comprensión lectora podría contribuir significativamente al desempeño en resolución de problemas matemáticos, especialmente cuando los estudiantes alcanzan niveles superiores de competencia lectora. Esto resalta la importancia de un enfoque integrado en la enseñanza, donde el desarrollo de habilidades lingüísticas avanzadas no se vea como completamente desconectado del desarrollo de competencias matemáticas. Los educadores podrían considerar estrategias específicas para desarrollar comprensión lectora avanzada como un medio para potenciar también el rendimiento en resolución de problemas matemáticos.
Finalmente, estos hallazgos contribuyen al campo de investigación educativa al evidenciar la complejidad de las relaciones entre diferentes dominios de aprendizaje, cuestionando modelos simplistas de relaciones lineales y sugiriendo la necesidad de considerar patrones de asociación más complejos y posiblemente no monotónicos entre diferentes habilidades cognitivas y de forma integral.
Conflicto de Intereses
Los autores declaran que no existen conflictos de intereses.
Referencias
Akın, A. (2022). Is reading comprehension associated with mathematics skills: A meta-analysis research. International Online Journal of Primary Education (IOJPE), 11(1), 47-61. https://doi.org/10.55020/iojpe.1052559
Anselmo, G. A.; Yarbrough, J. L.; Kovaleski, J. F. & Tran, V. N. (2017). Criterion‐related validity of two curriculum‐based measures of mathematical skill in relation to reading comprehension in secondary students. Psychology in the Schools, 54(9), 1148-1159. https://doi.org/10.1002/pits.22050
Antezana M., L. y Guarachi R., R. (2021). Comprensión lectora y resolución de problemas aritméticos en estudiantes de 5º curso del nivel primario. Revista Boliviana de Educación, 3(4), 37–51. https://doi.org/10.33996/rebe.v3i4.287
Acharya, B. R. (2017). Factors affecting difficulties in learning mathematics by mathematics learners. International Journal of Elementary Education, 6(2), 8-15. http://dx.doi.org/10.11648/j.ijeedu.20170602.11
Bae, Y. S.; Chiang, H. M. & Hickson, L. (2015). Mathematical word problem solving ability of children with autism spectrum disorder and their typically developing peers. Journal of Autism and Developmental Disorders, 45(7), 2200-2208. https://doi.org/10.1007/s10803-015-2387-8
Can, D. (2020). The Mediator Effect of Reading Comprehension in the Relationship between Logical Reasoning and Word Problem Solving. Participatory Educational Research (PER), 7(3), 230-246. https://doi.org/10.17275/per.20.44.7.3
Carballo, O. A. (2024). Impacto de la comprensión lectora en el aprendizaje de las matemáticas. RIDE Revista Iberoamericana para la Investigación y el Desarrollo Educativo, 14(28), 656-670. https://doi.org/10.23913/ride.v14i28.1899
Díaz B., F. y Hernández R., G. (2010). Estrategias docentes para un aprendizaje significativo. Una interpretación constructivista (3a.ed.). Mc Graw Hill.
Díaz L., J. A. y Díaz F., R. (2018). Los Métodos de Resolución de Problemas y el Desarrollo del Pensamiento Matemático. Bolema: Boletim de Educação Matemática, 32(60) 57-71. https://doi.org/10.1590/1980-4415v32n60a03
Hijada, M. V. & Dela Cruz, M. L. (2022). The gap between comprehension level and problem-solving skills in learning mathematics. Universal Journal of Educational Research, 1(1), 35–43. http://files.eric.ed.gov/fulltext/ED621118.pdf
Khalid, M. & Embong, Z. (2020). Sources and Possible Causes of Errors and Misconceptions in Operations of Integers. International Electronic Journal of Mathematics Education, 15(2), em0568. https://doi.org/10.29333/iejme/6265
Kintsch, W. (1998). Comprehension: A paradigm for cognition. Cambridge University Press.
Klotz, E.; Ehmke, T. & Leiss, D. (2025). Text comprehension as a mediator in solving mathematical reality-based tasks: The impact of linguistic complexity, cognitive factors, and social background. European Journal of Educational Research, 14(1), 23-39. https://doi.org/10.12973/eu-jer.14.1.23
Ministerio de Educación Nacional (2020). Lineamientos Curriculares de Matemáticas. https://www.mineducacion.gov.co/1780/articles-339975_matematicas.pdf
Montero, L. V. y Mahecha, J. A. (2020). Comprensión y resolución de problemas matemáticos desde la macroestructura del texto. Praxis & Saber, 11(26), 1-17. https://doi.org/10.19053/22160159.v11.n26.2020.9862
Nahdi, D. S.; Cahyaningsih, U.; Jatisunda, M. G. & Rasyid, A. (2023). Mathematics Interest and Reading Comprehension as Correlates of Elementary Students’ Mathematics Problem-Solving Skills. Edukasiana: Jurnal Inovasi Pendidikan, 3(1), 115–127. https://doi.org/10.56916/ejip.v3i1.510
Prasetyaningrum, A. & Yuniarti, Y. (2021). Usage of reading comprehension to enhance word problem solving skills in mathematics. Journal of English Educators Society, 6(2), 260-266. https://doi.org/10.21070/jees.v6i2.1380
Pérez, Y. y Ramírez, R. (2011). Estrategias de enseñanza de la resolución de problemas matemáticos: Fundamentos teóricos y metodológicos. Revista de Investigación, 35(73), 169-194. https://www.redalyc.org/articulo.oa?id=376140388008
Obina, J. E.; Tecson, R. Q.; Kalis, G. L. & Bura-ay, D. C. (2025). Investigating the Relationship of Reading Comprehension on the Solution Processes of Mathematical Word Problems. European Journal of Education Studies, 12(1), 183-203. http://dx.doi.org/10.46827/ejes.v12i1.5776
Organización para la Cooperación y el Desarrollo Económicos. (2023). PISA 2022 Results (Volume I and II) - Country Notes: Colombia (OECD iLibrary).
R Core Team (2021). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria.
Sánchez C., H. (2013). La comprensión lectora, base del desarrollo del pensamiento crítico. Horizonte de la Ciencia, 3(5), 31-38. https://www.redalyc.org/journal/5709/570960878005/html/
Schoenfeld, A. H. (1992). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics. In: D. A. Grouws (Ed.). Handbook of research on mathematics teaching and learning (pp. 334-370). Macmillan.
Snow, C. E. & Sweet, A. P. (2003). Reading for Comprehension. In: A. P. Sweet & C. E. Snow (Eds.). Rethinking Reading Comprehension (pp. 1-16). The Guilford Press.
Terrones, D. C.; Flores C., F.; Supo C., F. y Cerrillo Q., S. A. (2023). Estrategias de comprensión lectora y resolución de problemas matemáticos en estudiantes de primaria. Horizontes Revista de Investigación en Ciencias de la Educación, 7(27), 77–85. https://doi.org/10.33996/revistahorizontes.v7i27.498
Valero-Ancco, V. N., Pari-Orihuela, M. y Calsin-Chambilla, Y. M. (2024). Comprensión Lectora en Universitarios Ingresantes. Revista Tecnológica-Educativa Docentes 2.0, 17(1), 174-182. https://doi.org/10.37843/rted.v17i1.453
Vinces V., V. A.; Olmedo C., N. C.; Chamorro B., M. A.; Chamorro B., M. D-C. y Acosta B., V. J. (2024). La Comprensión Lectora y su Influencia en la Resolución de Problemas Matemáticos del Entorno en los Estudiantes de Octavo Año de Educación Básica. Ciencia Latina Revista Científica Multidisciplinar, 8(6), 1294-1310. https://doi.org/10.37811/cl_rcm.v8i6.14899
Woodcock, R. W. & Muñoz-Sandoval, A. F. (2001). Batería III Woodcock-Muñoz. Riverside Publishing.